I promised today I'd compare investing in things (like DIY equipment, or thermal windows, or a freezer for your bulk-purchased meat) with investing in financial thingamabobs (like savings accounts or CDs or IRAs).
Both in terms of the way we live and in terms of the math involved, there are some big differences between the two. And because life is complicated, the math could get really complicated if I let it. So I'm going to pretend that you have a bit of money to do something with, and you do only one thing. You either buy the battery charger, or else you put the money in the bank, but either way, you then forget you ever did it.
Either way, we start with a bit of money.
If, instead, you drop the money into a savings account or CD and earn interest, you don't lose your money. Interest has a way of seeming like nothing much happens at first (which is why it's hard/boring to invest money), but to take off like a rocket in later years (which is why every financial planner urges you to do it). This kind of graph is called "exponential"; it grows slow, then fast.
So, which of these two is better?
If you can earn better than 5% interest (after taxes!) right now, you know something I don't. So anything you buy that can earn its keep in just seven years is a darned wise purchase. Heck, if your choice right now is putting your money in a savings account or buying a gizmo that wouldn't pay for itself for a decade, I'd go for the gizmo. Even though it will take a quarter century to come out ahead, 25 years from now you'll be thanking me.
Which is all to say, that home economics is economics, too.
Both in terms of the way we live and in terms of the math involved, there are some big differences between the two. And because life is complicated, the math could get really complicated if I let it. So I'm going to pretend that you have a bit of money to do something with, and you do only one thing. You either buy the battery charger, or else you put the money in the bank, but either way, you then forget you ever did it.
Either way, we start with a bit of money.
If you buy something that's supposed to "pay for itself" someday, the immediate effect is that you've lost that money. In the short run, this is a losing prospect.
But over time, you earn that money back through savings. And more-or-less, you save the same amount of money each year, so the the way you make that money is "linear". That's the simplest kind of mathematical formula.
 |
| The graph of your money, if you depend on payback time. |
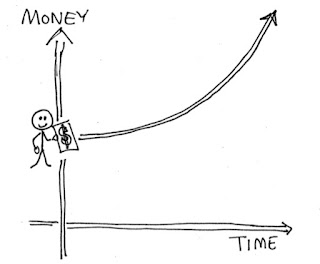 |
| The graph of your money, if you invest in a savings account. |
The answer is, it depends. It depends on how long your payback time is (things that can pay for themselves quickly are probably going to win out), but also on the interest you'd be earning.
If your payback time is long or the interest you could earn is high, then a savings account or a CD beats buying something. Our own home insulation project is a good example of this.
If your payback time is quick or your investment accounts don't earn that much, then some day (longer than the payback time), your CFL lightbulb purchase is going to win out over that T-bond. But note that if you continue to do nothing, eventually the savings wins again. Exponential functions rule.
 |
| Investing wins over buying the hybrid riding lawn mower. |
If your payback time is quick or your investment accounts don't earn that much, then some day (longer than the payback time), your CFL lightbulb purchase is going to win out over that T-bond. But note that if you continue to do nothing, eventually the savings wins again. Exponential functions rule.
 |
| Things that have a short payback time win out over savings, for a little while. But compound interest wins in the long run. |
Clearly, then, the best strategy would be to choose to buy things that could pay for themselves quickly enough to beat the IRA in those early sluggish years, and then move that money over into savings once it has created the great big pile burning holes in your pocket. So, how quick a payback time is quick enough?
Here's a table that shows various payback times. Against each, I list the highest possible interest it could ever beat, and also the amount of time it would take for the payback strategy to actually match an investment earning that interest rate.
| pay back time (years) | interest (%) | years for payback to get ahead of interest |
| 1 | 45 | 2.5 |
| 2 | 20 | 5 |
| 3 | 13 | 8 |
| 4 | 9.6 | 10 |
| 5 | 7.6 | 13 |
| 6 | 6.3 | 15 |
| 7 | 5.4 | 18 |
| 8 | 4.7 | 20 |
| 9 | 4.2 | 23 |
| 10 | 3.1 | 24 |
If you can earn better than 5% interest (after taxes!) right now, you know something I don't. So anything you buy that can earn its keep in just seven years is a darned wise purchase. Heck, if your choice right now is putting your money in a savings account or buying a gizmo that wouldn't pay for itself for a decade, I'd go for the gizmo. Even though it will take a quarter century to come out ahead, 25 years from now you'll be thanking me.
Which is all to say, that home economics is economics, too.


Sometimes the payback includes intangibles too, things that can't be measured on a graph, such as physical comfort or pride of place or helping someone. I like your graphs as I'm a visual learner. Thanks for sharing.
ReplyDeleteOn the intangibles: agreed, wholeheartedly! The money is really just a servant to other higher things (although sometimes we let the servant become the master). Glad you like the graphs -- I had fun drawing them. --MM
DeleteLove this article. I had the concept, but never made the numbers out.
ReplyDelete